Background Knowledge
강화학습이란, 제한된 환경 안에서 설정된 에이전트가 현재의 상태를 인식하고, 선택 가능한 행동들 중 보상을 최대화하는 행동 또는 행동 순서를 선택하는 방법을 말한다.
여기서 강화(Reinforcement)란 심리학에서 생물이 어떤 자극에 의해 미래의 행동을 바꾸는 것을 말한다.

- Environment : 관측이 가능하고, 통제할 수 있는 닫힌 공간
- Interpreter : 환경에서 Agent으로 가기 전, 확인하는 버퍼 단계로 보아도 무방하다 (프로그래머)
- Agent : 환경 내에서 제어되는 객체
- State : 환경 내에서 관측되는 Agent의 상태, Observation이라고 표현되기도 한다
- Action : Agent가 행동한 결과
- Policy : Agent가 취할 행동을 결정하는 방식, 알고리즘
- Value : State를 기반으로 결정한 값 (=Model이 예측한 값)
- Reward : Agent에게 돌려주는 보상
$ Q(s,a)=r(s,a)+γmaxaQ(s′,a) $
MDP(Markov Decision Process)
나의 행동이 보상과 이어지는 강화라는 연결 관계를 어떻게 수학적으로 표현할 수 있을까? 이전의 상태와 현재 상태가 연결되는 관계를 수학에서는 Markov State(마코프 상태)라고 표현한다. 강화학습에서는 행동에 따라 보상이 주어지는 시간적 연결이 핵심이기 때문에, 앞으로 볼 강화학습은 마코프 상태를 가정하여 진행한다.

마코프 상태에서는 상태를 나타내는 S, 행동을 A, 조건부 확률을 P, 상황(S)에 따라 행동(A)시의 보상을 R, 그리고 미래에 대한 감가율을 ᵞ(gamma)라고 표현한다. 그럼 이 MDP를 강화학습에 어떻게 적용시킬까??
How Models learn Reinforcement?
컴퓨터에서 강화학습이 이루어지는 원리는 벨만 방정식을 기반으로 한다. 벨만 방정식에서는 현재의 상태(state)와 행동(action), 그리고 다음 상태와 행동에 대한 관계식을 점화식으로 기술한다.

위에서 나온 수식들을 처음 보면 외계어처럼 당황스러울 수 있지만, 수식을 쉽게 풀어쓴다면 다음과 같다.
- R(a,s) : s 상태에서 a로 행동했을 때 예상되는 보상값
- V(s') : 다음 상태(s')에 대한 기댓값
- P(s,a,s') : s 상태에서 a로 행동했을 때 기대되는 s' 의 상태의 값
자세히 보면, V가 반복적으로 쓰이는 것을 보면서 재귀적인 구조를 띄는 것을 볼 수 있다.
강화학습에서는 행동 -> 보상(자극) -> 행동 변경이라고 했다.
강화학습에서의 보상(S) 상태에서 행동(A) 했을 때의 보상은 R(s,a)로 표현한다.
V는 상태와 행동에 대한 보상을 표현하는 함수로, 재귀적으로 쓰이면서 현재와 미래의 가치를 고려하는 함수이다.
쉽게 생각해볼 수 있는 예를 들어서 미로찾기를 생각해보자.

경로를 찾았을 때 보상을 1이고, 나머지 상황일 때 0이라고 가정한다면, 마지막 시간 t일 때
마지막에서 1단계 전은 t-1이므로,
그 다음 t-2, t-3, ... 시작까지 이르면
여기서 γ 값은 미래를 반영하는 비중으로 1이라면 현재 가치와 미래의 가치가 같은 것이고, 0이 된다면 미래는 전혀 반영되지 않은 구조가 된다.이 구조는 수학적으로 보면 점화식 구조를 지니고, 조금 더 생각하면 동적 프로그래밍도 가능한 게 보인다. 강화학습은 이렇게 점화식을 잘 설계하여 미래의 보상이 있다는 가정 하에 미래의 보상과 현재의 가치를 잘 고려해 판단하는 구조이다. 위의 미로에 다시 적용해본다면 학습을 진행하면서 보상이 반영이 잘 됐다면 길을 찾는 판단을 할 때, 이전에 성공했던 길을 잘 따라가게 될 것이다.
아래 그림은 Q-Table이라고 하여 상태와 행동 별로 갖는 가치를 테이블로 표현한 것으로 학습되면서 갱신되는 과정을 담았다.

실제로 학습을 진행해본다면 어떻게 진행하는게 맞을까?
강화학습에는 원하는 방향으로 가도록 보상을 갱신하는 방법 (Value-Based)과 정책을 잘 설정해 현재 가치만을 바라 볼 것이 아니라, 다음 상태까지 고려해 진행하는 방법(Policy-Based)이 있다.
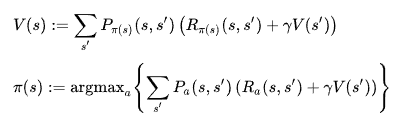
- 현재 상태에서 어떤 행동이 최선의 행동인지 판단하는 Policy Function
- 어떤 값이 최고의 보상을 줄 지 판단하는 Value Function
Policy Function과 Value Function의 차이를 비교해보자.
수식을 보았을 때 Policy Function에서는 Value Function이 나오고, Value Function에서는 Policy Function이 나와 서로 얽혀있어서 복잡해보인다. 원래는 서로 상호작용을 하면서 진행하지만 이해를 위해 이 부분은 제외하고 각자 최선의 상황을 찾아간다고 가정하자.
Policy Function은 현재 상황(s)가 주어졌을 때, 현재의 행동(a)에 따라 미래(s')의 모든 상황
Value Function은 현재 상황(s)이 주어졌을 때, Policy Function에서 판단한 정책
어떻게 보면, Value 기반으로 진행한다면 눈 앞에 이득(점수)만 있다면 쫓아가는 팩맨같다고 볼 수도 있다.

어떻게 보면, Policy는 닥터 스트레인지와 같다고 볼 수 있다.
(우린 14,000,605개의 경우의 수를 봤을 수도 있는 닥터 스트레인지를 설계하고 싶어한다)

강화학습을 여기서 조금 더 확장시켜보면 상태와 행동이 다양해지는 가정도 가능하다. 하지만 강화학습의 문제 중 하나는 우리가 생각하는 현실은 상태와 행동이 매우 다양해 표현하기 어렵다는 점이다. 강화학습을 설계하는 입장에선 팩맨처럼 눈 앞의 보상만 보다가 죽지 않아야 하고, 너무 미래를 바라보다 현재에 보상을 적게 두지 않아야 하기에 강화학습은 매우 신중한 설계가 필요하다.
용어 설명
앞으로 볼 강화학습에서는 Value Function, State-Value Function 등 영어와 수학적 표현이 많이 사용된다. 어떤 논문은 State를 기반으로 최적의 Policy를 측정하는 것이 목적일 수 있고, 다른 논문은 어떻게 행동했을 때 최적의 Value는 무엇인지 최적화하는 것이 목적일 수도 있다. 전자는 State를 기반으로 최적의 Policy를 측정해야 하는 Policy Gradient 관점에서 볼 수 있고, 후자는 Value를 기반으로 최적의 Policy를 측정하는 Greedy 관점에서 볼 수도 있다. 논문들에서 자주 사용 하는 용어들을 알아보자.
Value Function G(t), V(s)
Agent가 현재 상태에서 예상되는 보상을 Value Function이라 한다.
State-Value Function V(s)
위의 Value Function과 유사하지만, Policy를 포함해 특정 state에서 보상을 예상하는 함수를 의미한다.
Action-Value Function Q(s,a)
State-Value Function이 특정 state일 때의 보상을 예상하는 함수였다면, Action-Value Function은 특정 State에서, 특정한 Action을 했을 때의 보상을 예상하는 함수을 의미한다.
용어들 다음으로, 대략적인 방법론에 대해서 알아보자
Methods Summary
강화학습의 방법은 다양한 방법들이 존재하지만 대표적인 키워드로 분류하면 아래와 같다.
- Model-Free vs Model-Base
- Policy-Base vs Value-Base
- On-Policy vs Off-Policy
- Single Agent vs Multi Agent
- Centralization vs Decentralization ( Multi-Agent Reinforcement Learning )
Model-Free vs Model-Base
- Model-Base : 사용자가 환경에 대한 지식을 구축하고, 지식에 입각해 행동을 취하는 강화학습 방법
- Model-Free : actor에 대한 정책을 직접 생성하여 환경(environment) 내에서 관측되는 값을 end-to-end 학습하는 것
Policy-Base vs Value-Base
Policy-Base는 Agent가 State를 기반으로 판단하는 알고리즘에 초점에 두고, Value-Base는 Agent가 State의 가중치를 결정하는 알고리즘에 초점을 둔다.
Policy 정책이 완벽하다면, Value를 설정할 필요가 없고 Value 정책이 완벽하다면, Policy를 설정할 필요가 없다.
Value-based Model-free 알고리즘
현재 State 내에서 Value가 높은 곳으로 선택하는 알고리즘으로 예를 들면 Q-Learning 알고리즘이 있다. Value function이 Reward를 높이도록 설계되기 때문에 Reward=Value로 보아도 무방하다.
Policy-based Model-free 알고리즘
Agent가 얻는 Value값들 속에서 어떤 행동을 할지 확률을 고르는 알고리즘으로, 정책을 강화하기 위해 Gradient Ascent 방식을 사용한다.Value Function과 Policy Function 두 가지를 다 사용하는 경우도 있는데, 이는 Actor-Critic 모델이라 한다.
On-Policy vs Off-Policy
- On-Policy : Agent가 진행하는 즉시 학습해 정책에 반영되는 방식을 On-Policy라 한다
- Off-Policy :Agent가 진행하는 데이터를 Replay Memory로 기억해두었다가, 한꺼번에 학습하여 진행하는 방식을 Off-Policy라 한다. 학습 결과가 바로 반영되지 않는다는 점에서 On-Policy와 상반된다.
Single-Agent vs Multi-Agent
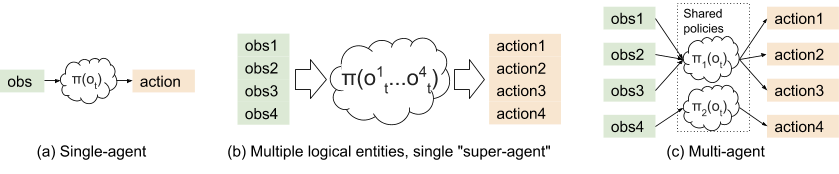
마지막으로, 대략적인 RL 알고리즘에 대한 개요는 다음과 같다.
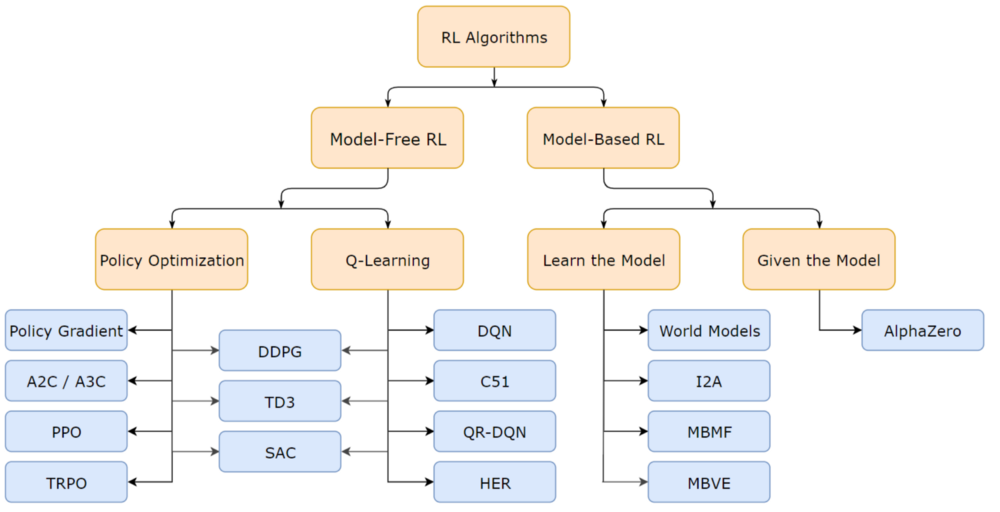
참고
https://dreamgonfly.github.io/blog/rl-taxonomy/#value-function
https://en.wikipedia.org/wiki/Markov_decision_process
'AI | ML > Reinforcement Learning' 카테고리의 다른 글
| [RL] 테트리스 강화학습 시도 내용 (0) | 2024.01.23 |
|---|---|
| [RL] DQN(Deep Q-Network) 논문 리뷰 (0) | 2024.01.18 |
| [ML-Agent] Unity 게임을 gym.Env 환경으로 변경 (0) | 2021.09.03 |
| pyMARL 구조 분석 + COMA 코드 분석 (0) | 2021.08.23 |
| [Unity] ML-Agents 설치 및 테스트해보기 (2) | 2021.08.13 |